72÷金利≒元本が2倍になる期間
たとえば3%の金利で複利運用した場合、資産が2倍になる期間は、
72÷3%≒24年
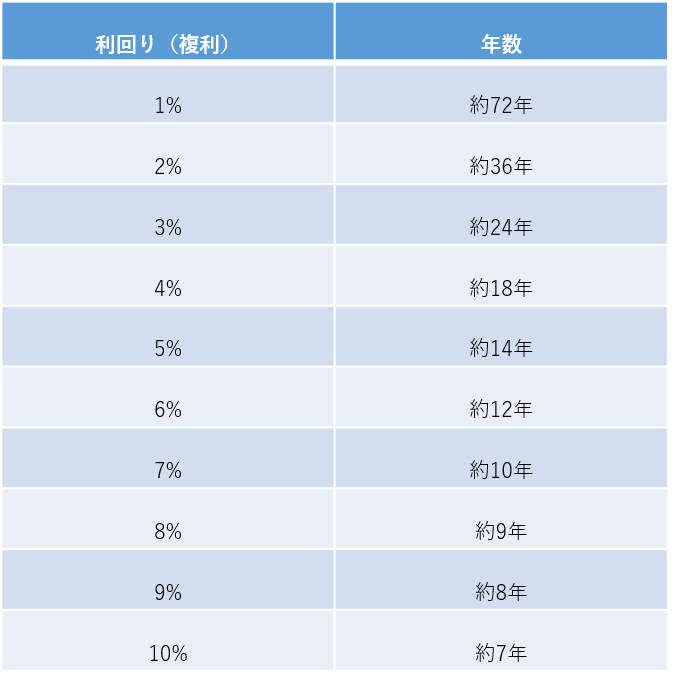
となります。金利と年数の関係は以下の通りです。(表「72の法則による金利と年数の関係」参照)
また、72を期間で割れば、資産を倍にするのに必要な利息を求めることができます。
たとえば、10年で資産を倍にしたい場合、必要な利回りは
72÷10年=年約7%
となります。
ちなみにこの7%は、米国株式市場の長期リターンに近い数字です。言い換えれば、米国株に長期投資をし、再投資し続ければ、10年で資産を倍にする可能性が高まるということになります。
複利効果
1年や2年という短い期間では、単利と複利の差はあまりありませんが、10年・20年と長期で運用した場合の差は大きくなります。
運用で得た利益は生活費などに使うのではなく、再投資しながら長期運用するようにしましょう。期間が長くなるほど複利効果を活かせます。
資産運用のコツは時間をかけてお金を増やしていくことです。
複利運用でお金を増やす仕組みができれば、あとは時間を味方にすることで、資金は大きくなっていくのです。
少額からでもいいので、できるだけ早い時期に投資を始めるようにしましょう。
個人金融資産1,800兆円の半分は現金・預金です。
しかし低金利が続いているので、定期預金でも年率0.01%しか金利がつきません。
定期預金では、100万円を倍の200万円にするのに、複利運用でも約7200年かかります(72÷0.01%≒7200年)。
しかし、株式や投資信託を年率3%で複利運用した場合、
72÷3%≒14年
年利3%なら約24年で2倍になります。
将来に備えてお金を増やすためには、預金ではなく、リスクを取りながら投資をする必要があるのです。
資産が3倍になる期間がわかる「115の法則」
資産が2倍になる期間がわかるのは72の法則でしたが、資産が3倍になる期間がわかるのは「115の法則」で、計算式は以下の通りです。
115÷運用利回り(複利)≒ 資産が3倍になる期間
たとえば、5%の利回りで運用した場合、資産が3倍になる期間は
115÷5≒23年
となります。
単利では「100の法則」
複利運用の「72の法則」、「115の法則」のほかに、単利の「100の法則」もあります。
100の法則では、単利で運用した場合に資産が2倍になる期間がわかります。計算式は以下の通りです。
100÷運用利回り(金利)≒お金が2倍になる期間
配当や金利を受け取った時、再投資せずに単利で運用を続けると、何年で資産を2倍にできるかがわかるのです。
たとえば5%の利回りの場合、複利では
72÷5≒14.4年
約14年で資産が2倍になりますが、単利では
100÷5≒20年
約20年かかる計算になります。
複利と単利では、利回り5%で資産を2倍にするのに約6年も差がついてしまうのです。
まとめ
今回は複利運用における「72の法則」について解説しました。
資産運用は複利効果を活かすべきですが、72の法則を使えば、資産が倍になるまでの年数を簡単に計算できます。
もちろん、株や投資信託では毎年の利回りが保証されておらず、税引き後のリターンも考慮する必要がありますが、おおよその目安として72の法則を利用するようにしましょう。
モトリーフール・ジャパン