「ねぇ、どうして数学なんて勉強しなくちゃいけないの?」――子どもにそう聞かれて困った経験がある、もしくは、自分自身がそう感じ続けてきた、という人も多いかもしれない。「AI時代になれば、めんどうな計算はぜんぶAIがやるんだから必要ないでしょ」という人もいる。しかし、発売1カ月半で6万部を突破した『東大の先生! 文系の私に超わかりやすく数学を教えてください!』の著者で、東京大学教授の西成活裕氏は「これからのAI時代にこそ、数学的な考え方が必要です」と話す。
西成先生は、42歳という若さで東大教授になった超エリートでありながら、「子どもにも学生にも大人たちにも数学を好きになってほしい!」という思いで数学の楽しさを広めている。そんな西成先生に、「数学が役に立つ理由」を教えてもらった。
数学は身の回りの困りごとを解決するためのツール
「こんなややこしい計算を覚えて、いったい何の役に立つの⁉」
学生時代、数学の授業にそんな疑問を抱えていた人は少なくないでしょう。数学アレルギーを持ってしまう理由のひとつは、「何がゴールなのかわからないまま授業が淡々と進む」こと、そしてもうひとつは「数学を学ぶ意味がわからない」ことではないかと思います。「どうせ社会に出たら役立たない」と感じてしまえば、学ぶ意欲が起こらないのは当然のことです。
ですが実際は、生活のあらゆる場面で数学は非常に役立ちます。そして、これからのAI時代において、数学的な考え方はますます必要になるでしょう。数学の知識がなくても生きていけることは確かですが、日常生活で数学を応用できる場面はたくさんあります。というよりも、もともと数学は、私たちの身の回りの困りごとを解決するためのツールとして生まれたのですから。
では、具体的にどのような場面で役立つのか、例を挙げてみましょう。
数学の知識を少し使えば有事の際にも大いに役立つ
たとえば、小さなお子さんがいて哺乳瓶を使用している家庭なら、その哺乳瓶を消毒する必要がありますよね。ですが、子どもがそろそろお腹を減らしそうなのに、いつも使っている市販の消毒液をうっかり切らしてしまった! というときはどうしましょう?
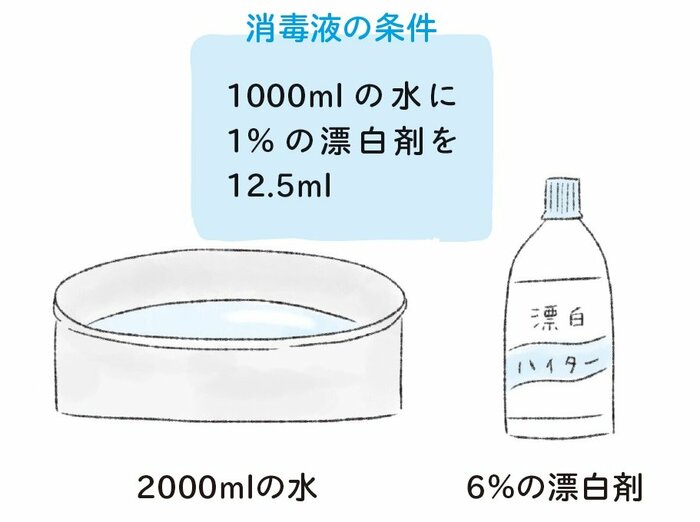
ネットで調べたところ、「1000㎖の水に対して1%の次亜塩素酸ナトリウム水溶液を12.5㎖入れたものを使えばいい」と書いてあったとします。家庭にある次亜塩素酸ナトリウム水溶液といえば、塩素系台所用漂白剤が代表的ですが、ボトルを見たら6%の水溶液だと書いてある。水は2000㎖用意しました。では、入れるべき漂白剤の量はどれくらいでしょう?〈別図版1参照〉
水が2倍になったワケですから、濃度を保つためには1%の水溶液も2倍の25㎖必要だということはわかりますよね。
でも手元にある漂白剤は6%なので、そのまま25㎖入れると6倍も濃くなってしまいます。それなら、25㎖を6で割ってしまえばいい。すると25÷6だから……「4㎖と少しになるだろうな」とわかります。難しい方程式などは必要なく、小学生の算数で解けるのです。
「発想が出てくるかどうか」がポイント
今の便利な世の中、計算しなくても代替策があるので、数学を使わなくてもいいケースがほとんどです。でも、数学の知識を少し使えば色々な状況に対処できたり節約ができたりしますし、有事の際などには大いに役立ちます。つまり、「数学は日常生活に役立たない」のではなく、「実生活の課題を数学で解こうという発想が出てくるかどうか」がポイントになるのです。
「有事の際」という話が出ましたが、日本にたびたび大きな被害を及ぼす津波の高さについても、数学で計算することができます。
私の専門の1つに「ソリトン理論」という波の動きを計算する特殊な数学の分野があります。国土交通省はこの理論をもとに津波の計算をしていて、「このエリアは防潮堤の高さをこのくらいにしないといけない」という数字を弾き出し、実際、東北地方に今とんでもなく巨大な防潮堤を建てています。
もちろん、安全面から見ると正解でも、もはや海が見えないほどの巨大な防潮堤は、景観的には不正解かもしれません。そういう意味では、世の中の問題は数学だけですべて解決できるわけではありません。ただ、1つの基準を提示することはできます。何の基準もなければ、各人が思い思いに話すだけで、議論がまとまりません。基準があるからこそ議論が前に進むのです。
頭がいい人の6つの「思考体力」
学生時代に数学で挫折した経験のある文系の人は、数学に対して高いハードルを感じている人も多いようです。ですが、論理を「言葉(自然言語)」で書いたのが国語で、「記号」で書いたのが数学というだけ。数学の授業で習う「公式」というものは、感覚としては「言語」を学んでいるのと同じです。
ですから、文系でも理系でも、説明の根底にあるロジックは共通していて、違うのは「どの言語を使うか」だけ。そこにそれほど大きな差はありません。
「でも、数学が得意な人って『頭がいい』イメージがあるよね」なんて声もよく聞かれますが、それは頭がいいから数学ができるのではなく、どちらかというと数学を学んでいくことによって頭が鍛えられるのだと思っています。
そもそも「頭がいい」というのは、どういうことでしょう? 私は、次の6つの「思考体力」の総合値だと考えます。
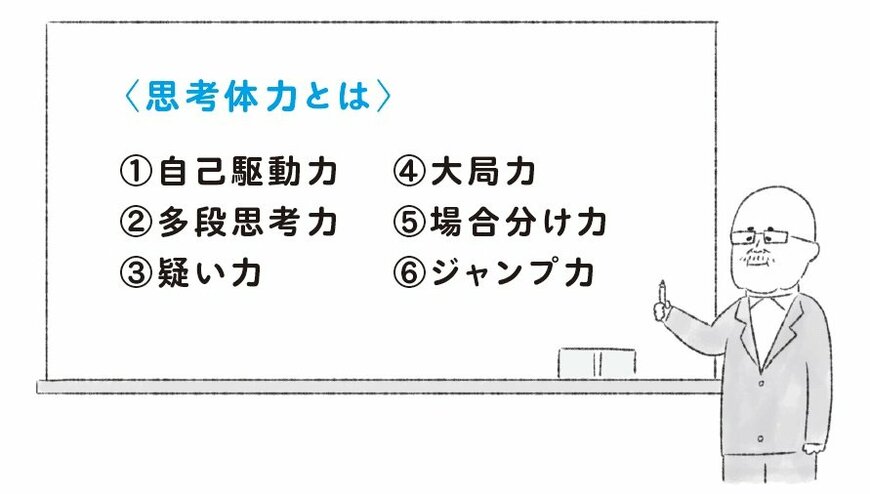
(1)自己駆動力
(2)多段思考力
(3)疑い力
(4)大局力
(5)場合分け力
(6)ジャンプ力
こうした力をまんべんなく持っている人ほど、複雑な課題を解決できる人だと思うのです〈別図版2参照〉。
数学で鍛えられる力
では、ひとつずつ説明していきましょう。
まず「(1)自己駆動力」はいわば思考のエンジンです。人は「知りたい」「解決したい」という思いが強いほど、がんばって考えますよね。たとえば数学もいきなり授業に入るのではなくて、たとえば野球が好きな子に、「外野フライが飛んできたとき、ボールの落下位置は二次関数でわかるんだよ」と教えるなど、「自分ごと」に感じてもらえば、自発的に学ぶきっかけになるでしょう。数学は、そういった自己駆動力も鍛えてくれます。
そして「(2)多段思考力」は、「AならB、BならC、CならD……」と、思考した結果をどんどん積み上げながら粘り強く考え続ける力、思考のスタミナみたいなもので、複雑な問題を解決するときに絶対に欠かせないものです。特に数学の場合はこの力がガンガン鍛えられます。
突飛な発想で課題解決をする力
そして「(3)疑い力」とは、自分の判断や答えを疑う力。頭の片隅に常に「冷静な自分」がいることで、計算ミスなどが一気に減ります。
「(4)大局力」は、空飛ぶ鳥の目線のように、物事全体を俯瞰して眺められる力のこと。大局から見るクセがあれば、大事なことを見落とす可能性が減ります。
次の「(5)場合分け力」は、複雑な課題で選択肢がたくさんあるときに、正しく評価する力のこと。数学だと、何か問題があって、それをどの数学のツールを使うと早く解けそうかと判断するような場合に使います。
最後の「(6)ジャンプ力」は「ひらめき」と言ってもいいでしょう。多段思考を何度も何度も積み上げていってもたどり着かないことがある。そんなときに、「え? このやり方で?」と突飛な発想をした結果、課題が解決できることがあるのです。
AIに使われる側か、AIを使いこなす側か
先の見えない現代では、思考体力をまんべんなく鍛える必要がありますし、そのために数学は最適なツールです。数学には、「問題を解決する最強の武器」であり、「社会人として必要な思考体力を身につけるための脳トレ」という大事な意味があるのです。しかも、一般的な社会人であれば、身につけて役に立つのは、ほぼ「中学数学レベル」だけでOK。そう難しいことはありません。
これからはAIがどんどん進化していき、数学的なことはすべて処理してくれるというイメージがあるかもしれませんが、結局、AIだって人間がプログラムしなければ動きません。AIに使われる側になるか、AIを使いこなす側になるかは、「思考体力」を鍛えられるかどうかにかかっているといえるのです。
いかがでしょう。これで、お子さんに「数学なんてなんで勉強しなきゃいけないの?」と聞かれたときには、堂々と 「数学が人生に役立つ理由」を教えてあげられるのではないでしょうか。
そして、みなさん自身も今から数学を学び直しても遅くはありません。ぜひ、思考体力を鍛えて、さらに生活の質をアップさせてくださいね。
■ 西成活裕(にしなり・かつひろ)
東京大学先端科学技術研究センター教授。専門は数理物理学、渋滞学。1967年東京都生まれ。東京大学工学部卒業、同大大学院工学研究科航空宇宙工学専攻博士課程修了。ドイツのケルン大学理論物理学研究所などを経て現職。予備校講師のアルバイトをしていた経験から「わかりやすく教えること」を得意とし、中高生から主婦まで幅広い層に数学や物理を教え、小学生にも微積分の概念を理解させた実績を持つ。著書『渋滞学』(新潮社)で講談社科学出版賞などを受賞したほか、『とんでもなく役に立つ数学』(KADOKAWA)、『東大人気教授が教える 思考体力を鍛える』(あさ出版)など著書多数。
西成氏の著書:
『東大の先生! 文系の私に超わかりやすく数学を教えてください!』
西成 活裕